BOOLEAN ALGEBRA

BOOLEAN ALGEBRA 

 

              Boolean algebra was introduced by George Boole in his first book "The Mathematical Analysis of Logic (1847)," and set forth more fully in his An Investigation of the Laws of Thought (1854).

 

             

       According to Huntington, the term "Boolean algebra" was first suggested by Sheffer in 1913, although Charles Sanders Peirce gave the title "A Boolean Algebra with One Constant" to the first chapter of his "The Simplest Mathematics" in 1880.[4] Boolean algebra has been fundamental in the development of digital electronics, and is provided for in all modern programming languages. It is also used in set theory and statistics.

 

 

     In mathematics and mathematical logic, Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0, respectively.

 

   USES :

 

        Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or logical Algebra.

 

 

  

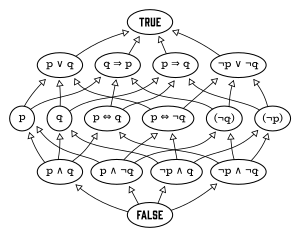
 DEFINITION:

 

             Boolean, or boolean logic, is a subset of algebra used for creating true/false statements. Boolean expressions use the operators AND, OR, XOR, and NOT to compare values and return a true or false result. These boolean operators are described in the following four examples: 

      # x AND y - returns True if both x and y are true; returns False if either x or y are false. 

     # x OR y - returns True if either x or y, or both x and y are true; returns False only if x and y are both false. 

    # x XOR y - returns True if only x or y is true; returns False if x and y are both true or both false. 

   # NOT x - returns True if x is false (or null); returns False if x is true.

 

 

Since computers operate in binary (using only zeros and ones), computer logic can often expressed in boolean terms. For example, a true statement returns a value of 1, while a false statement returns a value of 0. Of course, most calculations require more than a simple true/false statement.         

 

     Therefore, computer processors perform complex calculations by linking multiple binary (or boolean) statements together. Complex boolean expressions can be expressed as a series of logic gates.

 

            Boolean expressions are also supported by most search engines. When you enter keywords in a search engine, you can refine your search using boolean operators. 

             

                 For example, if you want to look up information about the Apple i Mac, but want avoid results about apples (the fruit) you might search for "Apple AND i Mac NOT fruit." This would produce results about i Mac computers, while avoiding results with the word "fruit." 

             

                While most search engines support boolean operators, their syntax requirements may vary. For example, instead of the words AND and NOT, the operators "+" and "-" .may be required .

 

 

RULES OF BOOLEAN  :

 

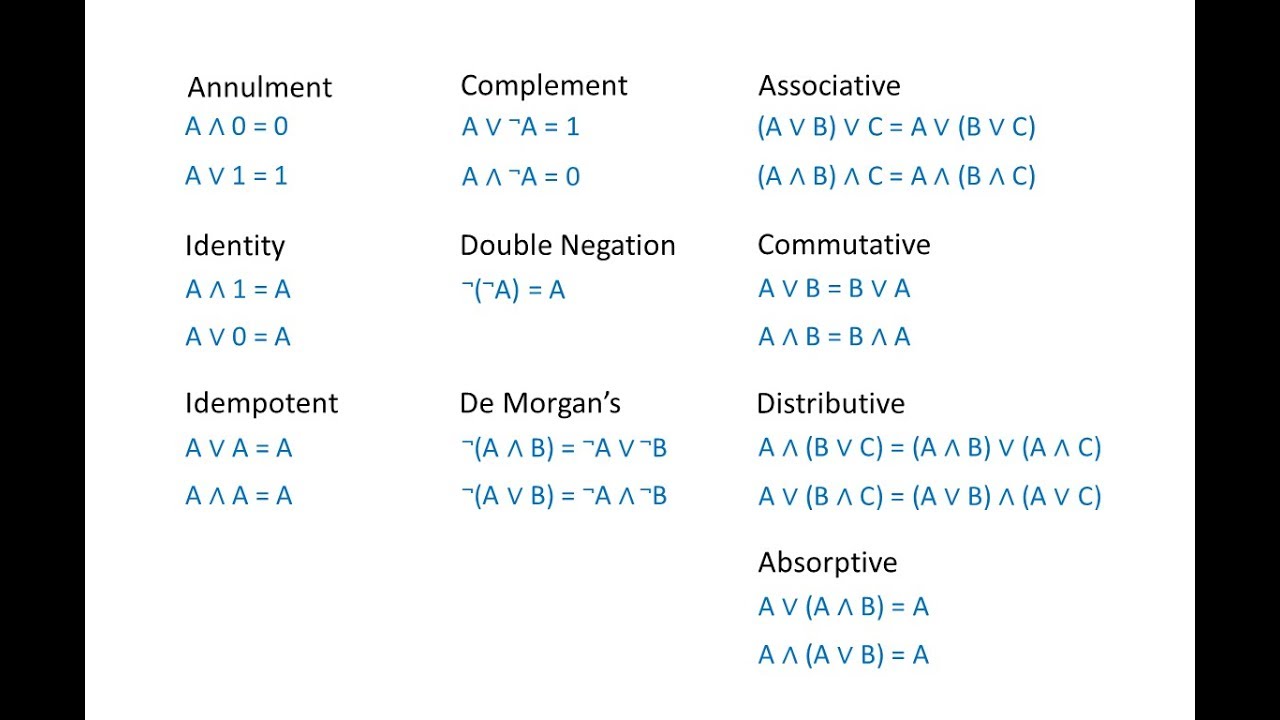
 1) Variables used can have only two values. Binary  1 for HIGH and binary 0 for LOW.

2) Complement of a variable is represented by an over bar (_). Thus complement of variable B is represented as (B bar). Thus if  B=0  then B bar =1 and vice versa.

3) OR of the variables is represented by a plus (+)  sign between them. For example : OR  of  A,B,C is represented as A+B+C.

4)  AND of the variables is represented by a dot (.). sign between them. For example : AND of A,B,C is represented as A.B.C  

 

 COMMUTATIVE LAW :

  

 

ASSOCIATIVE LAW  : 

 

 

 DISTRIBUTIVE LAW :